Original Article
, Volume: 15( 4)
Structure of M (I): Ternary Gamma-Semigroups
- *Correspondence:
- Madhusudhana Rao D, Associate Professor, Department of Mathematics, VSR & NVR college, Tenali, Guntut (Dt), Andhra Pradesh, India,Tel:9440358718;E-mail: [email protected]
Received:October 25, 2017;Accepted:November 20, 2017;Published:November 23, 2017
Citation:Vasantha M, Madhusudhana Rao D. Structure of M (I): Ternary Gamma-Semigroups. Int J Chem Sci. 2017;15(4):224
Abstract
The terms, ‘I-dominant’, ‘left I-divisor’, ‘right I-divisor’, ‘I-divisor’ elements, ‘M (I)-ternary Γ-semigroup’ for a ternary Γ-ideal I of a ternary Γ-semigroup are introduced and we characterized M (I)-ternary gamma semigroups.
Keywords
Completely prime ternary Γ -ideal; I-dominant element; I-dominant ternary Γ-ideal; I-divisor; M (I)-ternary Γ -semigroup
Introduction
In [1] introduced the concepts of A-potent elements, A-divisor elements and N (A)-semigroups for a given ideal A in a semigroup and characterized N (A)-semigroups for a pseudo symmetric ideal A. He proved that if M is a maximal ideal containing a pseudo symmetric ideal A, then either M contains all A-dominant elements or M is trivial. In this paper we extent these notions and results to M (I)-ternary Γ-semigroups.
Experimental
Preliminaries
Definition 2.1:Let T and Γ be two non-empty set. Then T is said to be a TernaryΓ-semigroupif there exist a mapping from T × Γ × T × Γ × T to T which maps (x1,α,x2,β,x3) → [x1αx2βx3] satisfying the condition: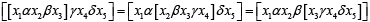 ∀ xi∈ T 1≤ i ≤ 5 and α,β,γ,δ∈Γ. A nonempty subset A of a ternary Γ-semigroup T is said to be ternary Γ-ideal of T if b,c∈T, α,β∈Γ, a∈A implies bαcβa∈ A,bαaβc∈ A,aαbβc∈ A. A is said to be a completely primeΓ提供理想的T x, y, z∈T和xΓyΓz⊆implies either x∈ A or y∈A or z∈ A. and A is said to be aprimeΓ-idealof T provided X,Y,Z are Ternary Γ-ideal of T and XΓYΓZ⊆A⇒X⊆A or Z⊆A. A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be a completely semiprimeΓ-ideal provided
∀ xi∈ T 1≤ i ≤ 5 and α,β,γ,δ∈Γ. A nonempty subset A of a ternary Γ-semigroup T is said to be ternary Γ-ideal of T if b,c∈T, α,β∈Γ, a∈A implies bαcβa∈ A,bαaβc∈ A,aαbβc∈ A. A is said to be a completely primeΓ提供理想的T x, y, z∈T和xΓyΓz⊆implies either x∈ A or y∈A or z∈ A. and A is said to be aprimeΓ-idealof T provided X,Y,Z are Ternary Γ-ideal of T and XΓYΓZ⊆A⇒X⊆A or Z⊆A. A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be a completely semiprimeΓ-ideal provided for some odd natural number n>1 implies
for some odd natural number n>1 implies Similarly, A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be semiprime ternary Γ-ideal provided X is a ternary Γ- ideal of T and
Similarly, A ternary Γ-ideal A of a ternary Γ-semigroup T is said to be semiprime ternary Γ-ideal provided X is a ternary Γ- ideal of T and for some odd natural number n implies X ⊆ A [2-6].
for some odd natural number n implies X ⊆ A [2-6].
Definition 2.2:A ternary Γ-ideal I of a ternary Γ-semigroup T is said to be pseudo symmetric provided x, y, z ∈T, I implies
I implies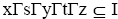 for all s, t ∈T and I is said to be semi pseudo symmetric provided for any odd natural number n,x∈T,
for all s, t ∈T and I is said to be semi pseudo symmetric provided for any odd natural number n,x∈T,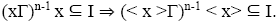
Theorem 2.3:Let I be a semi-pseudo symmetric ternaryΓ-ideal of a ternaryΓ-semigroup T. Then the following are equivalent.
1) I1=The intersection of all completely prime ternaryΓ-ideals of T containing I.
2) I11=The intersection of all minimal completely prime ternaryΓ-ideals of T containing I.
3) 111I=最小完全semiprime ternaryΓ-ideal of T relative to containing I.
4) I2={x ∈ T: (xΓ)n-1x ⊆I for some odd natural number n}
5) I3=The intersection of all prime ternaryΓ-ideals of T containing I.
6) I31=The intersection of all minimal prime ternaryΓ-ideals of T containing I.
7) I113=The minimal semiprime ternaryΓ-ideal of T relative to containing I.
8) I4={x ∈ T: (
Theorem 2.4:If I is a ternaryΓ-ideal of a semi simple ternaryΓ-semigroup T, then the following are equivalent. 1) I is completely semiprime.
2) I is pseudo symmetric.
3) I is semi-pseudo symmetric.
Results and Discussion
M (i)-ternary gamma-semigroup
We now introduce the terms I-dominant element and I-dominant ternary Γ-ideal for a ternary Γ-ideal of a ternary Γ- semigroup [7].
Definition 3.1:Let I be a ternary Γ-ideal in a Ternary Γ-semigroup T. An element x∈T is said to be I-dominant provided there exists an odd natural number n such that A ternary Γ-ideal J of T is said to be I-dominant ternary Γ- ideal provided there exists an odd natural number n such that
A ternary Γ-ideal J of T is said to be I-dominant ternary Γ- ideal provided there exists an odd natural number n such that
Note 3.2:If I is a ternary Γ-ideal of a ternary Γ-semigroup T, then every element of I is a I-dominant element of T and I itself an I-dominant ternary Γ-ideal of T.
Definition 3.3:Let I be a ternary Γ-ideal of a ternary Γ-semigroup T. An I-dominant element x is said to be a nontrivial Idominant element of T if x ∉ I.
Notation 3.4:Mo(I)=The set of all I-dominant elements in T.
M1(I)=The largest ternary Γ-ideal contained in Mo(I).
M2(I)=The union of all I-dominant ternary Γ-ideals.
Theorem 3.5:If I is a ternary Γ-ideal of a ternary Γ-semigroup T, the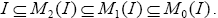
Proof: Since I is itself an I-dominant ternary Γ-ideal, and M2(I) is the union of all I-dominant ternary Γ-ideals. Therefore, I⊆M2(I). Let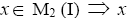 belongs to at least one I-dominant ternary Γ-ideals
belongs to at least one I-dominant ternary Γ-ideals is an I-dominant element. Hence, x∈M0(I). Therefore,
is an I-dominant element. Hence, x∈M0(I). Therefore, Clearly M2(I) is a ternary Γ-ideal of T. Since M1(I) is the largest ternary Γ-ideal contained in Mo(I), we have
Clearly M2(I) is a ternary Γ-ideal of T. Since M1(I) is the largest ternary Γ-ideal contained in Mo(I), we have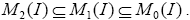 Hence,
Hence,
Theorem 3.6:If I is a ternary Γ-ideal in a ternary Γ-semigroup T, then the following are true.
1. M0(I)=I2.
2. M1(I) is a semiprime ternary Γ-ideal of T containing I.
3. M2(I)=I4.
Proof:(1) Mo(I)=The set of all I-dominant elements
(2) Suppose that for some odd natural number n. Suppose, if possible
for some odd natural number n. Suppose, if possible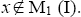 M1(I), < x > are the ternary Γ-ideals implies
M1(I), < x > are the ternary Γ-ideals implies is a ternary Γ-ideal. Since M1(I) is the largest ternary Γ-ideal in M0(I), We have
is a ternary Γ-ideal. Since M1(I) is the largest ternary Γ-ideal in M0(I), We have Hence, there exists an element y such that
Hence, there exists an element y such that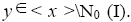 Now
Now for some odd natural number
for some odd natural number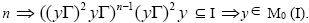 It is a contradiction. Therefore, x ∈ M1(I). Hence, M1(I) is a semiprime ternary Γ-ideal of T containing I.
It is a contradiction. Therefore, x ∈ M1(I). Hence, M1(I) is a semiprime ternary Γ-ideal of T containing I.
(3) Let x∈M2(I). Then there exists an I-dominant ternary Γ-ideal J such that x∈J.
J is I-dominant ternary Γ-ideal implies there exists an odd natural number n such that
 for some odd
for some odd Therefore,
Therefore,
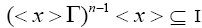 for some odd n∈ N. So < x > is an I-dominant ternary Γ-ideal in T and hence,
for some odd n∈ N. So < x > is an I-dominant ternary Γ-ideal in T and hence,
 Therefore,
Therefore, Hence,
Hence, It is natural to ask whether M1(I)=I3. This is not true.
It is natural to ask whether M1(I)=I3. This is not true.
Example 3.7:In the free ternary Γ-semigroup T over the alphabet x, y, z. For the ternary Γ-ideal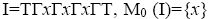
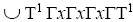 and
and But
But is a prime ternary Γ-ideal, let I, J, K are three ternary Γ-ideals of T such that
is a prime ternary Γ-ideal, let I, J, K are three ternary Γ-ideals of T such that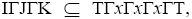 implies all words containing
implies all words containing or all words containing
or all words containing or all words containing
or all words containing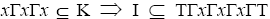 or
or Therefore,
Therefore, is a prime ternary Γ-ideal. We have
is a prime ternary Γ-ideal. We have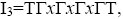 so
so Therefore, we can remark that the inclusions in
Therefore, we can remark that the inclusions in may be proper in an arbitrary ternary Γ-semigroup [8-11].
may be proper in an arbitrary ternary Γ-semigroup [8-11].
Theorem 3.8:If I is a semi pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T, then M0(I)=M1(I)=M2(I).
Proof:Suppose I is a semi pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. By theorem 3.7, M0(I)=I2and M2(I)=I4. Also by theorem 2.10, we have I2=I4. Hence, M0(I)=M2(I). By the theorem 3.5, We have
We have Now let
Now let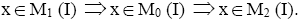 Therefore,
Therefore, Hence,
Hence,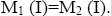 Therefore,
Therefore,
Theorem 3.9:For any semi pseudo symmetric ternary Γ-ideal I in a ternary Γ-semigroup T, a nontrivial I-dominant element 不能简单半(12,13].
不能简单半(12,13].
Proof:Since x is a nontrivial I-dominant element, there exists an odd natural number n such that Since I is semi pseudo symmetric ternary Γ-ideal, we have
Since I is semi pseudo symmetric ternary Γ-ideal, we have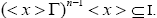 If x is semi simple, then
If x is semi simple, then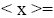
 and hence,
and hence, this is a contradiction. Thus, x is not semi simple.
this is a contradiction. Thus, x is not semi simple.
Theorem 3.10:If I is a ternary Γ-ideal in a ternary Γ-semigroup T, such that M0(I)=I, then I is a completely semiprime ternary Γ-ideal and I is a pseudo symmetric ternary Γ-ideal.
Proof:Let and
and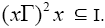 Since
Since Thus, there exists an odd natural number n such that
Thus, there exists an odd natural number n such that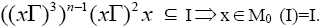 Therefore, I is a completely semiprime ternary Γ-ideal. By corollary 2.11, A is pseudo symmetric ternary Γ-ideal. Hence, I is completely semiprime and pseudo symmetric ternary Γ-ideal.
Therefore, I is a completely semiprime ternary Γ-ideal. By corollary 2.11, A is pseudo symmetric ternary Γ-ideal. Hence, I is completely semiprime and pseudo symmetric ternary Γ-ideal.
Theorem 3.11:If I is a semi pseudo symmetric ternary Γ-ideal of a ternary semi simple Γ-semigroup then I=M0(I).
Proof:Clearly,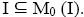 Let
Let If
If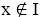 then x is a nontrivial I-dominant element. By theorem 3.9, x cannot be semi simple. It is a contradiction. Therefore,
then x is a nontrivial I-dominant element. By theorem 3.9, x cannot be semi simple. It is a contradiction. Therefore, and hence,
and hence, Thus
Thus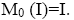
We now introduce a left I-divisor element, lateral I-divisor element, right, I-divisor element and I-divisor element corresponding to a ternary Γ-ideal A in a ternary Γ-semigroup.
Definition 3.12:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element is said to be a left I-divisor (a lateral I-divisor, right I-divisor) provided there exist two elements
is said to be a left I-divisor (a lateral I-divisor, right I-divisor) provided there exist two elements such that
such that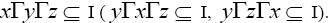
Definition 3.13:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element x∈T is said to be two-sided A-divisor if x is both a left I-divisor and a right, I-divisor element.
Definition 3.14:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. An element x∈T is said to be I-divisor if a is a left Idivisor, a lateral I-divisor and a right, I-divisor element.
We now introduce a left I-divisor ternary Γ-ideal, lateral I-divisor ternary Γ-ideal, right I-divisor ternary Γ-ideal and I-divisor ternary Γ-ideal corresponding to a ternary Γ-ideal I in a ternary Γ-semigroup.
Definition 3.15:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. A ternary Γ-ideal J in T is said to be a left I-divisor ternary Γ-ideal (lateral I-divisor ternary Γ-ideal, right I-divisor ternary Γ-ideal, two sided I-divisor ternary Γ-ideal) provided every element of J is a left I-divisor element (a lateral I-divisor element, a right I-divisor element, it is both a left I-divisor ternary Γ-ideal and a right I-divisor ternary Γ-ideal).
Definition 3.16:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. A ternary Γ-ideal J in T is said to be I-divisor ternary Γ-ideal provided if it is a left I-divisor ternary Γ-ideal, a lateral I-divisor ternary Γ-ideal and a right I-divisor ternary Γ-ideal of a ternary Γ-semigroup T.
Notation 3.17:Rl(I)=The union of all left I-divisor ternary Γ-ideals in T.
Rr(I)=The union of all right I-divisor ternary Γ-ideals in T.
Rm(I)=The union of all lateral I-divisor ternary Γ-ideals in T.
 We call R (I), the divisor radical of T.
We call R (I), the divisor radical of T.
Theorem 3.18:If I is any ternary Γ-ideal of a ternary Γ-semigroup T, then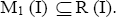
Proof:Let Since
Since we have
we have for some odd natural number n. Let n be the least odd natural number such that
for some odd natural number n. Let n be the least odd natural number such that If n=1 then x∈I and hence,
If n=1 then x∈I and hence,
If n >1, then where
where
Hence, x is an I-divisor element. Thus, Therefore,
Therefore,
Theorem 3.19:If I is a ternary Γ-ideal in a ternary Γ-semigroup T, then R (I) is the union of all I-divisor ternary Γ-ideals in T.
Proof:Suppose I is a ternary Γ-ideal in a ternary Γ-semigroup T.
Let J be I-divisor ternary Γ-ideal in T. Then J is a left I-divisor, a lateral I-divisor and a right I-divisor ternary Γ-ideal in T. Thus and
and
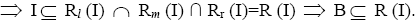
Therefore, R (I) contains the union of all I-divisor ternary Γ-ideals in T. Let Then
Then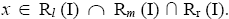 So
So
Hence, is I-divisor ternary Γ-ideal. So, R (I) is contained in the union of all divisor ternary Γ-ideals in T. Thus R (I) is the union of all divisor ternary Γ-ideals of T.
is I-divisor ternary Γ-ideal. So, R (I) is contained in the union of all divisor ternary Γ-ideals in T. Thus R (I) is the union of all divisor ternary Γ-ideals of T.
Corollary 3.20:If I is a pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T, then R (I) is the set of all I-divisor elements in T.
Proof:Suppose I is a pseudo symmetric ternary Γ-ideal in T. Let x be I-divisor element in T. Then where y, z
where y, z I is pseudo symmetric
I is pseudo symmetric
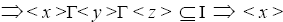 is I-divisor ternary Γ-ideal
is I-divisor ternary Γ-ideal
 Hence, R (I) is the set of all I-divisor elements in T. We now introduce the notion of M (I)-ternary Γ- semigroup.
Hence, R (I) is the set of all I-divisor elements in T. We now introduce the notion of M (I)-ternary Γ- semigroup.
Definition 3.21:Let I be a ternary Γ-ideal in a ternary Γ-semigroup T. T is said to be a M (I)-ternary Γ-semigroup provided every I-divisor is I-dominant.
Notation 3.22:Let T be a ternary Γ-semigroup with zero. If I={0}, then we write R for R (I) and M for M0(I) and M-ternary Γ-semigroup for M (I)-ternary Γ-semigroup.
Theorem 3.23:If T is an M (I)-ternary Γ-semigroup, then R (I)=M1(I).
Proof:Suppose T is an M (I)-ternary Γ-semigroup. By theorem 3.18,
Let is an I-divisor
is an I-divisor is an I-dominant
is an I-dominant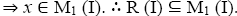
Hence,
Theorem 3.24:Let I be a semipseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. Then T is an M (I)-ternary Γ- semigroup iff R (I)=M0(I).
Proof:Since I is a semi-pseudo symmetric ternary Γ-ideal, by theorem 3.8, M0(I)=M1(I)=M2(I). If Tan M (I)-ternary Γ- semigroup, then by theorem 3.23, R (I)=M1(I). Hence, R (I)=N0(I). Conversely suppose that R (I)=M0(I). Then clearly every I-divisor element is an I-dominant element. Hence, T is an M (I)-ternary Γ-semigroup.
Corollary 3.25:Let I be a pseudo symmetric ternary Γ-ideal in a ternary Γ-semigroup T. Then T is an M (I)-ternary Γ- semigroup if and only if R (I)=M0(I).
Proof:因为每一个伪对称三进制Γ理想semi-pseudo symmetric ternary Γ-ideal, by theorem 3.24, R (I)=M0(I).
Corollary 3.26:Let T be a ternary Γ-semigroup with 0 and < 0 > is a pseudo symmetric ternary Γ-ideal. Then R=M iff T is an M-ternary Γ-semigroup.
Proof:The proof follows from the theorem 3.24.
Theorem 3.27:If N is a maximal ternary Γ-ideal in a ternary Γ-semigroup T containing a pseudo symmetric ternary Γ-ideal I, then N contains all I-dominant elements in T or T\N is singleton which is I-dominant.
Proof:Suppose N does not contain all I-dominant elements.
Let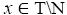 be any I-dominant element and y be any element in T\N.
be any I-dominant element and y be any element in T\N.
Since N is a maximal ternary Γ-ideal,
Since we have
we have Let n be the least positive odd integer such that
Let n be the least positive odd integer such that Since I is a pseudo symmetric ternary Γ-ideal then I is a semipseudo symmetric ternary Γ-ideal and hence,
Since I is a pseudo symmetric ternary Γ-ideal then I is a semipseudo symmetric ternary Γ-ideal and hence,
Therefore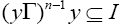 and hence, y is I-dominant element. Thus, every element in T\N is I-dominant.
and hence, y is I-dominant element. Thus, every element in T\N is I-dominant.
Similarly, we can show that if m is the least positive odd integer such that Therefore, there exists an odd natural number p such that
Therefore, there exists an odd natural number p such that for all
for all
Let x, y, z ∈ T\N. Since N is maximal ternary Γ-ideal, we have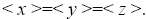
So So
So and hence, x ∈ sΓyΓt for some s, t ∈ T1. Now since I is a pseudo symmetric ternary Γ-ideal,
and hence, x ∈ sΓyΓt for some s, t ∈ T1. Now since I is a pseudo symmetric ternary Γ-ideal,
we have, If y ≠ x then s, t ∈ T. If s, t ∈ N then
If y ≠ x then s, t ∈ T. If s, t ∈ N then
这是不正确的。在这两种情况下我们反对tradiction. Hence, x=y.
Similarly, we show that z=x.
Corollary 3.28:If N is a nontrivial maximal ternary Γ-ideal in a ternary Γ-semigroup T containing a pseudo symmetric ternary Γ-ideal I. Then M0(I) ⊆N.
Proof:Suppose in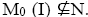 Then by above theorem 3.27, N is trivial ternary Γ-ideal. It is a contradiction. Therefore, M0(I) ⊆N.
Then by above theorem 3.27, N is trivial ternary Γ-ideal. It is a contradiction. Therefore, M0(I) ⊆N.
Corollary 3.29:If N is a maximal ternary Γ-ideal in a semi simple ternary Γ-semigroup T containing a semipseudo symmetric ternary Γ-ideal I. Then M0(I) ⊆N.
Proof:By theorem 3.11, I is pseudo symmetric ternary Γ-ideal. If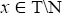 is I-dominant, then x cannot be semi simple. It is a contradiction. Therefore, M0(I) ⊆ N.
is I-dominant, then x cannot be semi simple. It is a contradiction. Therefore, M0(I) ⊆ N.
Conclusion
According to theorem 3.11, I is pseudo symmetric ternary Γ-ideal. If x ∈ T\N is I-dominant, then x cannot be semi simple. Hence, is a contradiction. Therefore, M0(I) ⊆ N.
References
- Anjaneyulu A.Stucture and ideals theory of semigroups. Thesis, ANU.1980.
- MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. Pseudo symmetric Γ-Ideals in Γ-semigroups. Int J Math Eng.2011;116:1074-81.
- MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. Prime Γ-radicals in Γ-semigroups. Int J Math Eng.2011;116:1074-81.
- MadhusudhanaRao D, Anjaneyulu A,GangadharaRao A. N(A)-Γ-semigroups.Ind J Math Mathemat Sci.2011;7(2):75-83.
- MadhusudhanaRao D. Primary ideals in quasi-commutative ternary semigroups. Int J Pure Alg. 2011;3(7):254-8.
- MadhusudhanaRao D, SrinivasaRao G. A Study on ternary semirings. IntJ Mathemat Arch. 2014;5(12):24-30.
- MadhusudhanaRao D, SrinivasaRao G. Special elements of a ternary semiring. Int J Eng Res and App.2014;4(11):123-30.
- MadhusudhanaRao D, SrinivasaRao G. Concepts on ternary semirings. International Journal of Modern Science and Engineering Technology (IJMSET).2014;1(7):105-10.
- MadhusudhanaRao D, Vasantha M,VenkateswaraRao M. Structure and study of elements in ternary Γ-semigroups. Int J Eng Res.2014;4(4):197-202.
- MadhusudhanaRao D. N (A)-ternary semigroups. African J Math and Comp Sci Res. 2013;6(7):149-55.
- Subramanyeswarao VB, Anjaneyulu A, MadhusudhanaRao D. Partially ordered Γ-semigroups.Int JEng Res Technol.2012;1(6):1-11.
- Sarala Y,Anjaneyulu A,MadhusudhanaRao D. Ternary semigroups. Int JMathematSciTechnol and Human.2013;76:848-59.
- Vasantha M, MadhusudhanaRao D. Properties of prime ternary-radicals in ternary-semigroups. Global Journal of Pure and Applied Mathematics.2015;1(6):4255-71.