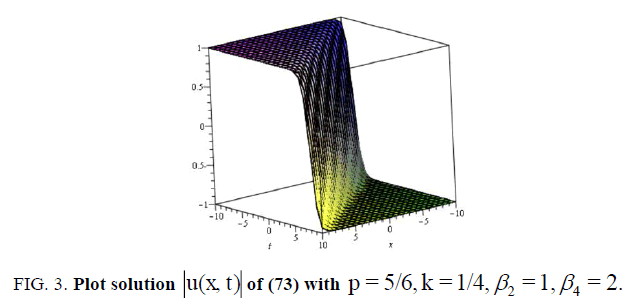原文
,卷:6(2)
求解高阶非线性丁格方程Schrà ¶的广义Kudryashov方法和一般Exp -函数方法
收到:2017年3月3日;接受:2017年5月4日;发表:2017年5月8日
引用:Zayed EME, al - nowewhy AG。广义Kudryashov方法及一般经验α求解高阶非线性Schrödinger方程的函数法。宇航学报。2017;6(2):120。
摘要
本文利用广义Kudryashov方法和广义Exp函数方法,得到了描述光脉冲在光纤中传播的具有四阶色散和三次五次非线性的非线性Schrödinger方程的许多新的精确解、对称双曲Fibonacci函数解、明孤子解、暗孤子解和奇异孤子解,以及自吸效应和自频移效应。我们比较了这两种方法的结果。并将本文的结果与已知的结果进行了比较。
关键字
广义Kudryashov方法;一般经验值α函数方法;具体解决方案;对称双曲斐波那契函数解;亮、暗、奇异孤子解;具有四阶色散和三次五次非线性的非线性Schrödinger方程
简介
物理和工程中的许多重要现象,如流体动力学、等离子体、化学、生物学、光纤等,都是借助数学物理中的非线性偏微分方程来描述的。研究这些非线性偏微分方程的精确解将有助于我们更好地理解这些现象。近年来,人们开发了各种有效的方法来构造这些方程的精确解。因此,偏微分方程的精确求解方法变得越来越重要,产生了诸如Hirota双线性变换方法[1]映射方法[2-function方法[3.,4],正余弦法[5,6]均质平衡法[7,8] tanh-sech法[9,10]扩展tanh-coth法[11,12],即(G’/G) -展开法[13-15]修正的简单方程法[16-19多重exp-function方法[19-21]第一积分法[22,23]孤子安萨兹法[24-28]广义Kudryashov方法[29-31[参考答案一般的α-函数法[32理性的;理性的G’/G) -展开法[33等等。
本文的目的是应用广义Kudryashov方法和一般的经验α给出了四阶色散、三次五次非线性非线性Schrödinger方程的许多新的精确解、对称双曲Fibonacci函数解以及明孤子解、暗孤子解和奇异孤子解[34-36]:
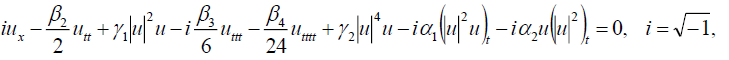 (1)
(1)
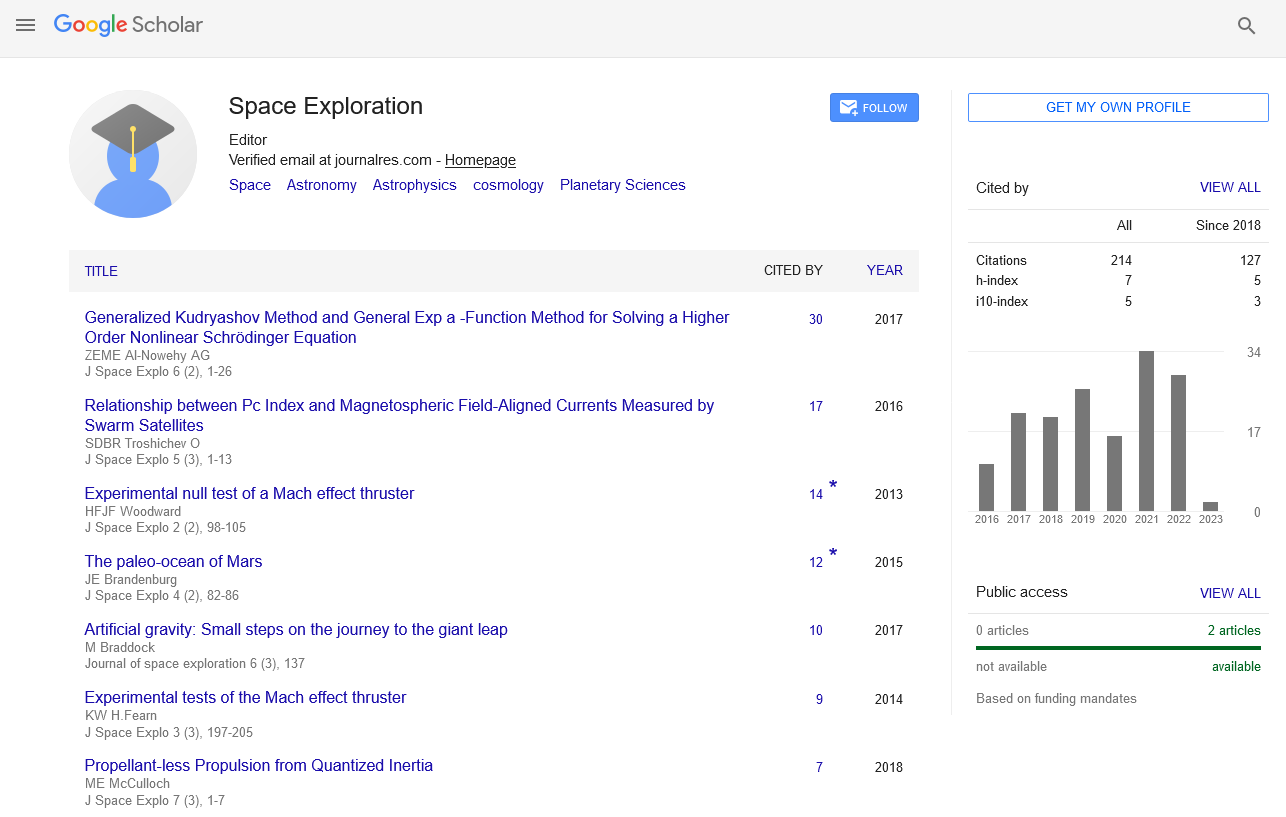
在哪里u=u(x t)为复包络振幅,t表示时间(在群速度框架内),x表示沿传播方向的距离(纵坐标),β2,β3.,β4分别表示群速度色散(GVD)、三阶色散(TOD)和四阶色散(FOD), γ1和γ2是介质的三次和五次非线性系数。这一项与α成比例1由非线性偏振慢变部分的一阶导数得到的结果。它负责脉冲边缘的自浸泡和激波形成。最后一项与α成比例2其自频移是由延迟拉曼响应引起的,通常α2应该是复杂的。当β3.=β4=γ2=α1=α2=0 Eq.(1)化简为著名的非线性Schrödinger方程。在很多情况下Imα2< <重新α2,所以我们考虑α的实部2如在[34].超短光脉冲在光纤中的传播由具有四阶色散和三次-五次非线性(1)的非线性Schrödinger方程控制。方程(1)已在[34]采用辅助方程法,在[35]采用f展开法,并在[36]采用孤子ansatz方法结合Jacobi椭圆方程方法。
本文组织如下:在第2节和第3节中,我们描述了广义Kudryashov方法和一般的经验α函数的方法。在第4节中,我们应用这两种方法求出了许多新的精确解、对称双曲Fibonacci函数解以及式(1)的明孤子解、暗孤子解和奇异孤子解。在第5节中,给出了一些结果的图形表示。第6节阐述了一些结论。
广义Kudryashov方法的描述
假设一个非线性偏微分方程具有以下性质:
F (u.ut,用户体验,utt,uxt,uxx……) = 0, (2)
在哪里u=u(x t)为未知函数,F是一个多项式u以及它的偏导数,其中涉及到最高阶导数和非线性项。
广义Kudryashov方法的主要步骤[29-31]的描述如下:
步骤1
首先,我们使用波变换:
u(x t) =U(ξ), ξ =kx+ λt, (3)
其中k和λ为任意常数,且k λ≠0,将式(2)化简为关于变量ξ ξ的形式为
H(U, U”、“U”,,…) = 0,
其中H是U(ξ)的多项式和它的总导数U, U”,“U”的,……这样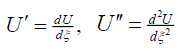 等等。
等等。
步骤2
我们假设ODE(4)的形式解可以写成如下有理形式:
 (3)
(3)
在哪里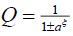 ,
,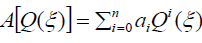 而且
而且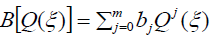 .函数Q是方程的解
.函数Q是方程的解
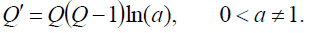 (6)
(6)
由(5)和(6)可知
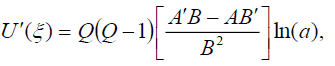 (7)
(7)
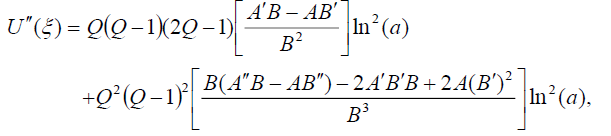 (8)
(8)
等等。
步骤3
我们确定这些值米而且n在式(5)中,通过平衡式(4)中U(ξ)的最高阶非线性项和最高阶导数,我们可以确定公式米而且n.
步骤4
我们将(5)-(8)代入Eq.(4),并使的所有系数相等问我(i = 0,1,2,…)到0,产生一个代数方程组,可以用Mathematica或Maple来求解,以找到k,λ和的系数一个我(i = 0,1,…n),bj(j = 0,1,…米).因此,我们可以得到式(2)的精确解。
所获得的解将依赖于[中给出的对称双曲斐波那契函数32,37].对称斐波那契正弦、余弦、正切和余切函数分别定义为:
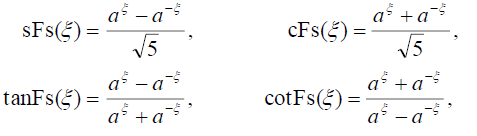 (9)
(9)
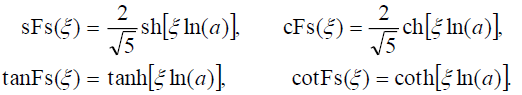 (10)
(10)
通用Exp的描述α函数的方法
参考[3.他和Wu已经建立了求解许多非线性偏微分方程的著名的exp-function方法。在本节中,我们给出一般Exp的主要步骤α-函数法[32]如下:
步骤1
我们考虑第2节的第(2)-(4)项。
步骤2
根据通用Expα-函数法,由Ali和Hassan提出[32],我们假设式(4)的波解可以表示为:
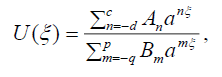 (11)
(11)
在哪里P q c d是正整数吗一个nB米也是常数,而0 < a≠1是一个任意的固定正数。我们可以把(11)写成如下的等价形式
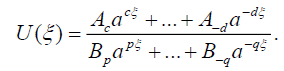 (12)
(12)
步骤3
我们确定的值c、p将式(4)的最高阶线性项与最高阶非线性项进行平衡。类似地,我们确定的值d,问将式(4)的最低阶线性项与最低阶非线性项进行平衡。
步骤4
将(12)代入式(4),计算的所有系数一个jξ(j = 0,±1,±2,…)将所有系数设为0,我们得到了一组可以用Maple进行求解的代数方程。因此,我们可以得到式(2)的精确解。
得到的解将取决于(9)和(10)中给出的对称双曲斐波那契函数。
应用程序
在本节中,我们应用广义Kudryashov方法和一般的经验α用第2节和第3节中描述的-函数方法求解以下各节中的式(1):
关于用广义Kudryashov方法求解式(1)
现在让我们用广义库德里亚绍夫方法求解式(1)。为此,我们使用波变换:
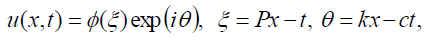 (13)
(13)
在哪里磷、钾而且c都是常数,∅(ξ)是ξ的实函数。将(13)代入式(1),分离实部和虚部,得到两个ode:
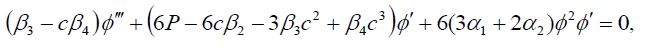 (14)
(14)
而且
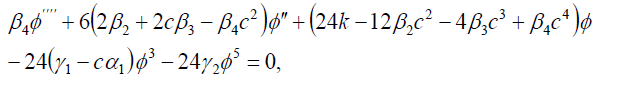 (15)
(15)
在哪里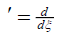 ,
,
有两种情况需要考虑:
案例1
如果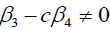 .
.
在这种情况下,微分Eq.(14)并将结果代入Eq.(15),我们得到非线性ODE:
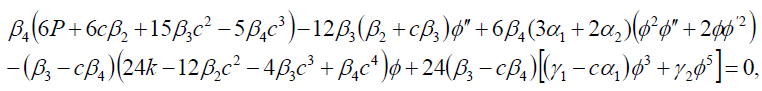 (16)
(16)
平衡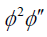 而且
而且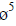 由式(16)可得关系式:
由式(16)可得关系式:
(2(n -m)+ (n -m)+ 2 = 5(n -m)⇒n = m+1。
如果我们选择米= 1,n= 2,则由(5)式(16)的形式解为:
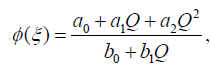 (18)
(18)
因此,
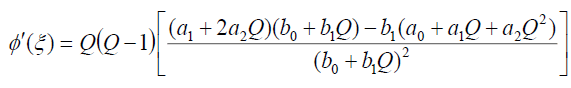 ln (a)、(19)
ln (a)、(19)
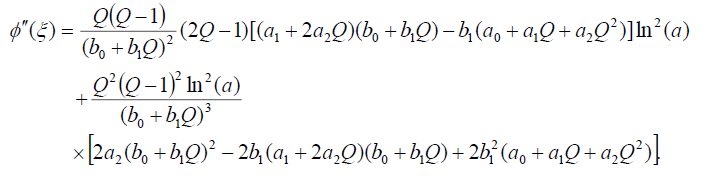 (20)
(20)
将式(18)-(20)代入式(16),取的各次幂的系数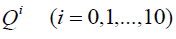 将每个系数设为0,我们得到一个代数方程组。利用Maple求解该代数方程组,得到以下集合:
将每个系数设为0,我们得到一个代数方程组。利用Maple求解该代数方程组,得到以下集合:
组1
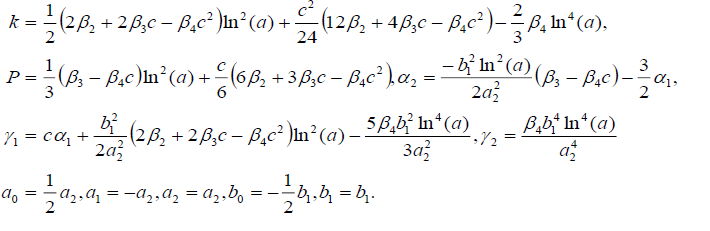
将式(21)代入式(18),得到式(16)的精确解:
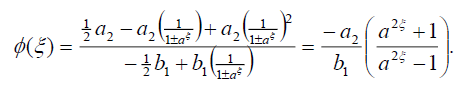 (22)
(22)
借助于(9)和(10),式(1)的双曲斐波那契函数解为:
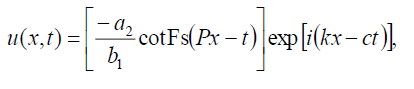 (23)
(23)
什么可以写在这个表格里
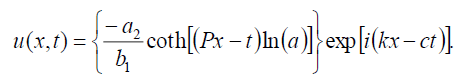 (24)
(24)
组2
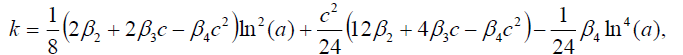
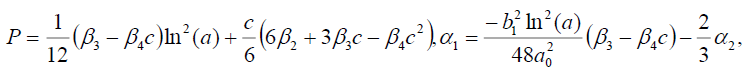 (25)
(25)
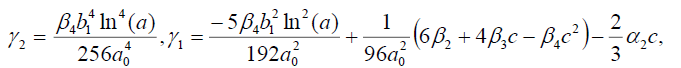
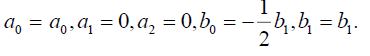
将(25)代入(18)可得精确解:
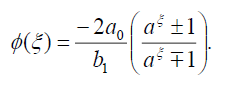 (26)
(26)
现在,式(1)孤子解的形式为:
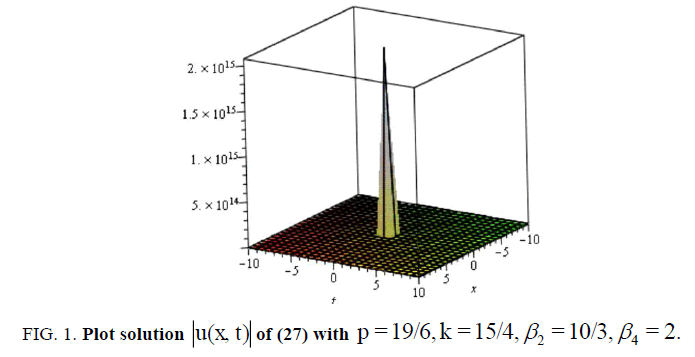
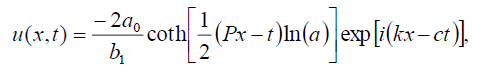 (27)
(27)
而且
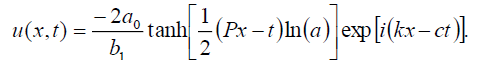 (28)
(28)
集3
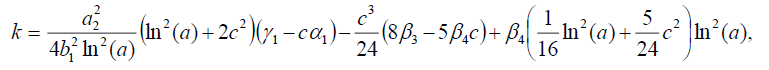
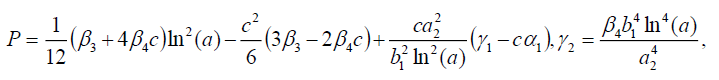 (29)
(29)
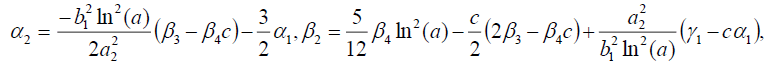
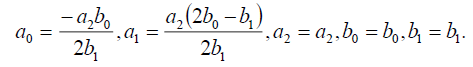
将(29)代入(18)可得精确解:
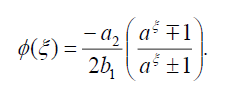 (30)
(30)
现在,式(1)孤子解的形式为:
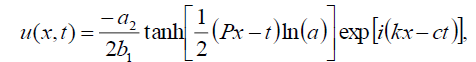 (31)
(31)
而且
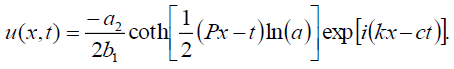 (32)
(32)
组4
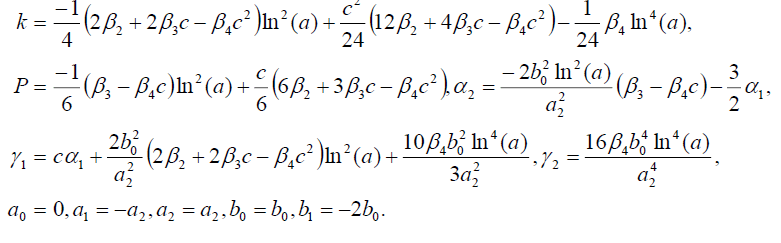 (33)
(33)
将(33)代入(18)可得精确解:
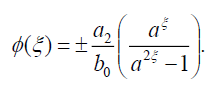 (34)
(34)
现在,式(1)的奇异孤子解形式为:
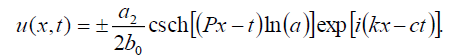 (35)
(35)
集合5
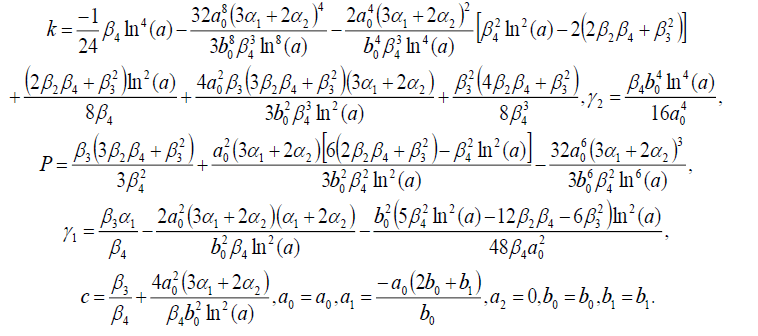 (36)
(36)
将(36)代入(18)可得精确解:
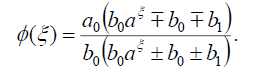 (37)
(37)
如果b1= 0则有式(1)孤子解的形式为:
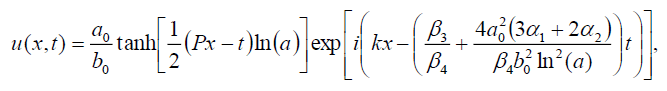 (38)
(38)
而且
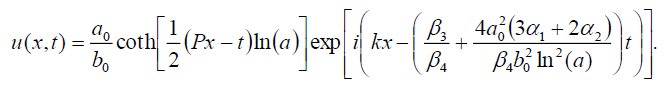 (39)
(39)
案例2
如果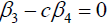 ,则有:
,则有:
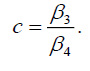 (40)
(40)
在这种情况下,等式。(14)和(15)成
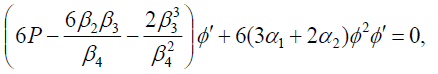 (41)
(41)
而且
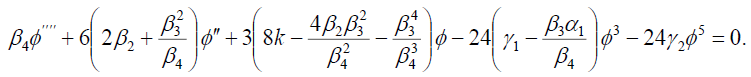 (42)
(42)
由式(41)可知:
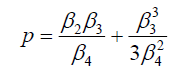 ,
,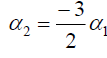 .(43)
.(43)
平衡ø”“和ø5由式(42)可得关系式:
(n - m)+ 4= 5(n - m)⇒n=米+ 1。
如果我们选择米= 1,n= 2,则式(42)的形式解与式(18)的形式相同。将式(18)-(20)代入式(42),取Q各次幂的系数我(i = 0,1,…,10),并将每个系数设为0,我们得到一个代数方程组。用Maple求解该代数方程组,得到以下集合:
组1
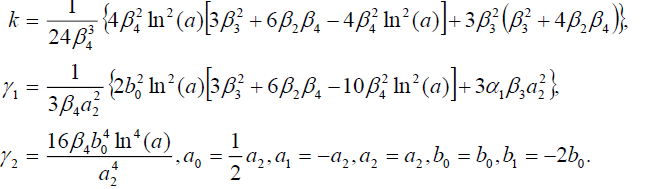 (45)
(45)
将式(45)代入式(18),得到式(42)的精确解:
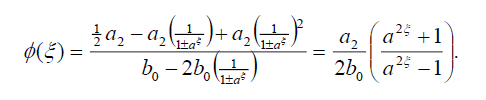 (46)
(46)
现在,借助(9)和(10),式(1)的双曲斐波那契函数解为:
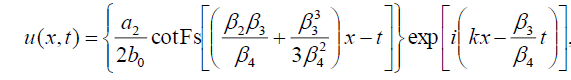 (47)
(47)
什么可以写在这个表格里
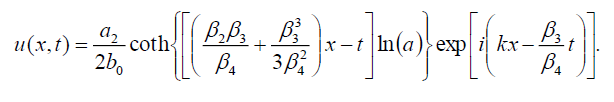 (48)
(48)
组2
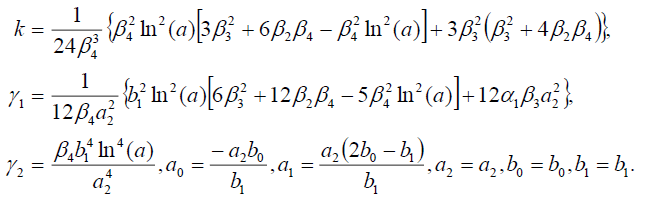 (49)
(49)
将(49)代入(18)可得精确解:
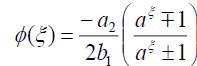 .(50)
.(50)
现在,式(1)孤子解的形式为:
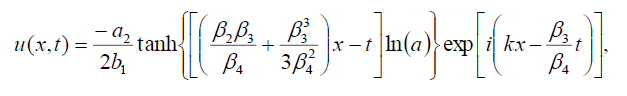 (51)
(51)
而且
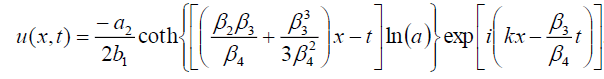 .(52)
.(52)
集3
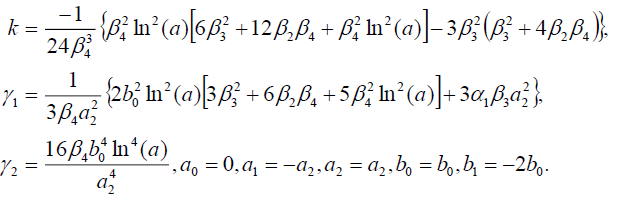 (53)
(53)
将(53)代入(18)可得精确解:
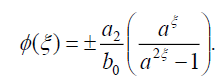 (54)
(54)
现在,式(1)的奇异孤子解形式为:
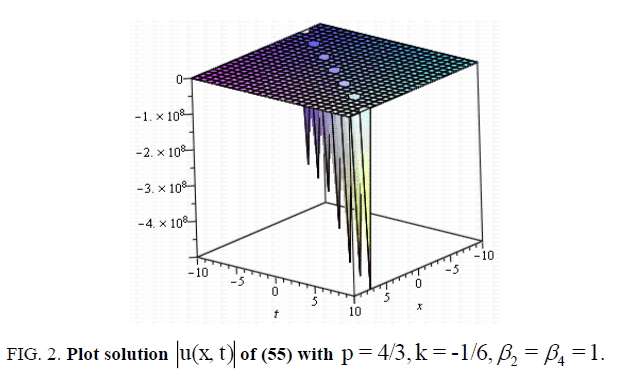
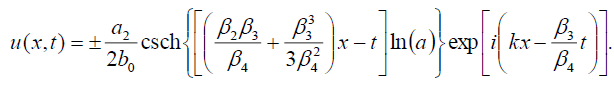 (55)
(55)
组4
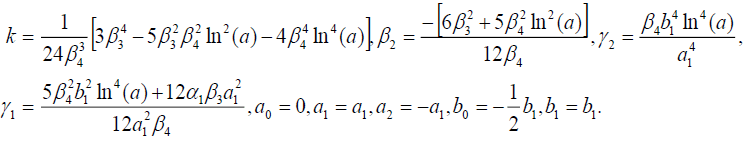 (56)
(56)
集合4的结果与集合3的结果有互换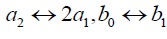 .
.
集合5
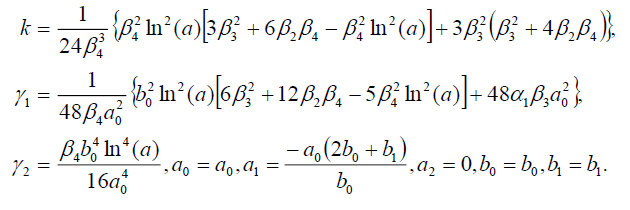 (57)
(57)
将式(57)代入式(18),可得精确解:
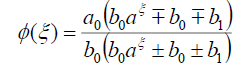 .(58)
.(58)
如果b1= 0则有式(1)孤子解的形式为:
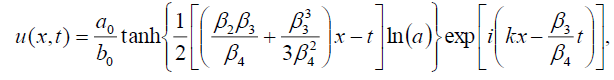 (59)
(59)
而且
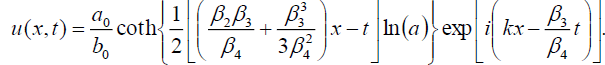 (60)
(60)
用一般的Exp求解式(1)α函数的方法
在本小节中,我们使用一般的Exp来求解Eq. (1)α函数的方法。为此,我们使用相同的变换(13)得到两个ode(14)和(15)。
有两种情况需要考虑:
情况下
如果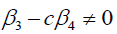 .
.
在本例中,将(14)插入(15)以获得ODE(16)。现在我们来确定正整数P q c d式(11)的。为了这一目标,我们平衡了最高的秩序 而且
而且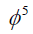 在(16)得到
在(16)得到
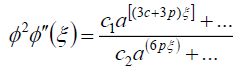 , (61)
, (61)
而且
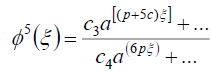 .(62)
.(62)
在哪里c我(我=1- 4)我是常数。由(61)和(62)可知
3c+3p = p +5c, (63)
结果是什么
p = c.(64)
用同样的方法,来确定的值d,问,我们平衡的最低阶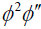 而且
而且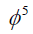 在(16)得到
在(16)得到
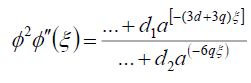 (65)
(65)
而且
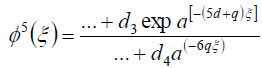 , (66)
, (66)
在哪里d我(我=1- 4)我是常数。由(65)和(66)可知
-(3 d + 3 q) = (q + 5 d), (67)
结果是什么
问=d.(68)
简单起见,我们设p=c= 1,问=d= 1。因此式(16)有形式解:
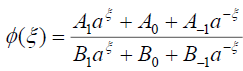 (69)
(69)
在哪里一个我B我(我= 0,±1)是后面要确定的常数。将(69)代入式(16),收集的所有系数一个jξ(j= 0,±1,…,±5),并使它们等于0,我们就得到了一组代数方程。在Maple的帮助下求解这些代数方程,我们有以下集合:
组1
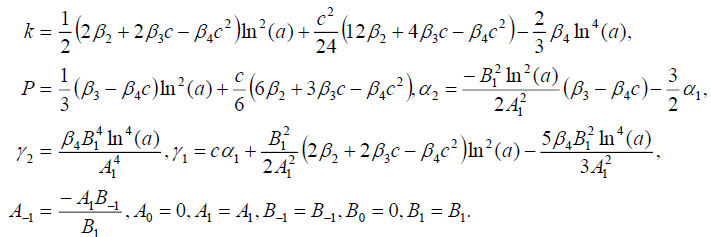 (70)
(70)
将式(70)代入式(69)可得式(16)的精确解
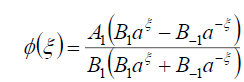 (71)
(71)
如果,B-1=B1则借助(9)和(10),式(1)的双曲斐波那契函数解为:
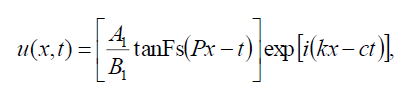 (72)
(72)
什么可以写在这个表格里
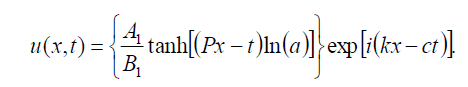 (73)
(73)
如果B-1=B1则借助(9)和(10),式(1)的双曲斐波那契函数解为:
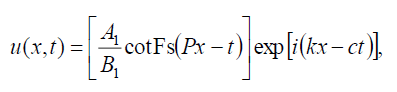 (74)
(74)
什么可以写在这个表格里
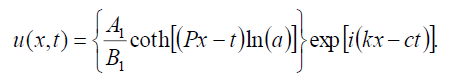 (75)
(75)
哪一个等价于前面的奇异孤子解(24),如果一个1= -一个2,B1=b1.
组2
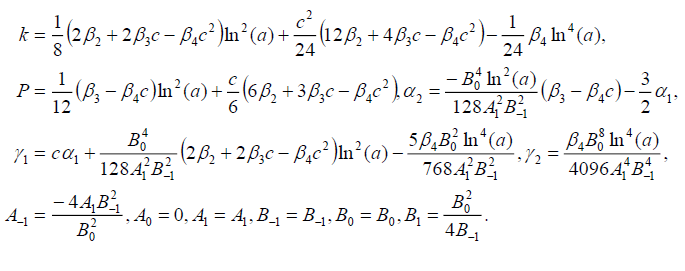 (76)
(76)
将式(76)代入式(69)可得式(16)的精确解
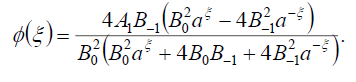 (77)
(77)
如果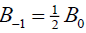 ,则式(1)的暗孤子解为:
,则式(1)的暗孤子解为:
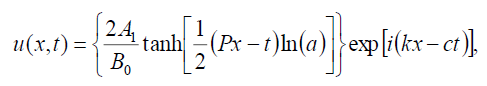 (78)
(78)
如果,哪个与前面的解(28)是等价的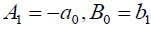 .
.
如果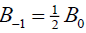 ,则式(1)的奇异孤子解为:
,则式(1)的奇异孤子解为:
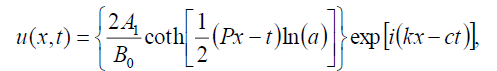 (79)
(79)
哪一个等价于前面的奇异孤子解(27),如果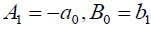
集3
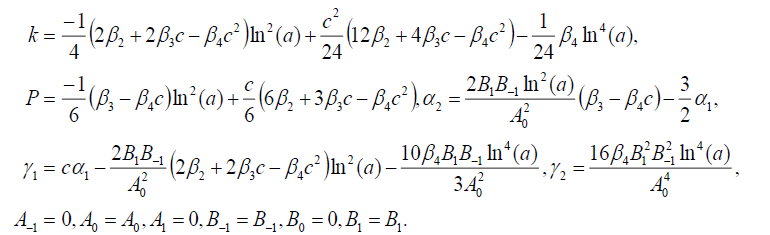 (80)
(80)
将式(80)代入式(69)可得式(16)的精确解
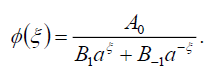 (81)
(81)
如果B-1=B1,则式(1)的亮孤子解为:
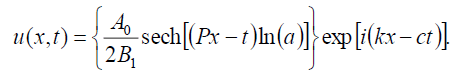 (82)
(82)
如果B-1=B1,则式(1)的奇异孤子解为:
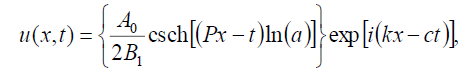 (83)
(83)
哪一个等价于前面的奇异孤子解(35),如果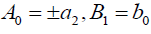 .
.
组4
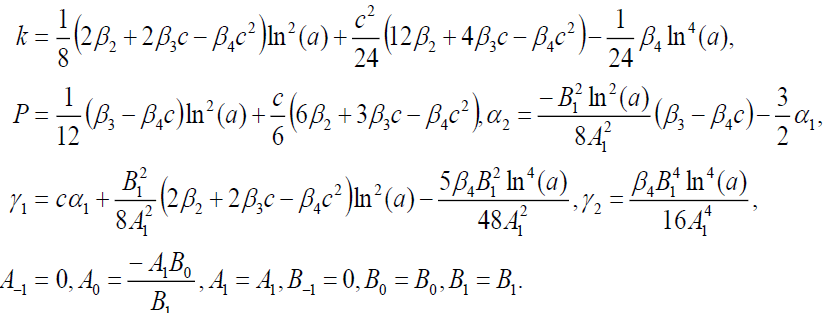 (84)
(84)
将式(84)代入式(69)可得式(16)的精确解
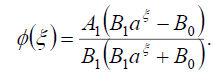 (85)
(85)
如果B0=B1,则式(1)的暗孤子解为:
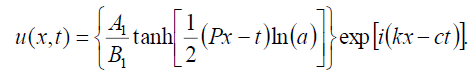 (86)
(86)
如果B0=- b1,则式(1)的奇异孤子解为:
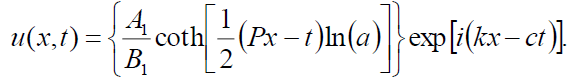 (87)
(87)
集合5
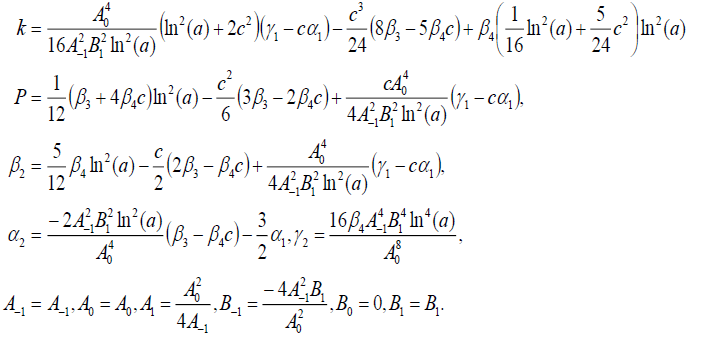 (88)
(88)
将式(88)代入式(69)可得式(16)的精确解
 .(85)
.(85)
如果 ,则式(1)的暗孤子解为:
,则式(1)的暗孤子解为:
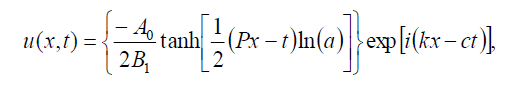 (90)
(90)
哪一个等价于前面的暗孤子解(31),如果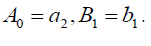
如果 ,则式(1)的奇异孤子解为:
,则式(1)的奇异孤子解为:
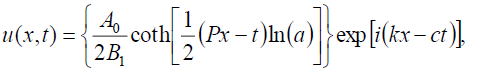 (91)
(91)
哪一个等价于前面的奇异孤子解(32),如果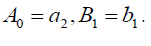
案例2
如果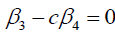 .
.
在本例中,我们使用与第4.1小节中的情形2相同的步骤来获得ODE(42)。现在我们来确定正整数P q c d式(11)的。为了这一目标,我们平衡了最高的秩序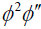 而且
而且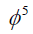 在(42)得到
在(42)得到
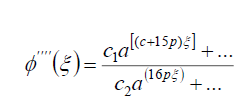 (92)
(92)
而且
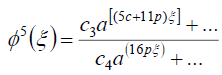 (93)
(93)
在哪里c我(我=1- 4)是常数。由(92)和(93)可知
c+ 15p= 5c +11p, (94)
结果是什么
p=c
用同样的方法,为了确定d q的值,我们平衡最小阶的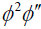 而且
而且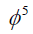 在(42)得到
在(42)得到
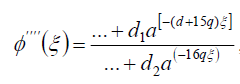 , (96)
, (96)
而且
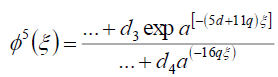 (97)
(97)
在哪里d我(我=1- 4)我是常数。由式(96)和式(97)可得
-(d+ 15问) = (5d+ 11问), (98)
结果是什么
问=d.(99)
简单起见,我们设p=c= 1,问=d= 1。因此式(42)有相同的形式解(69)。将(69)代入式(42),收集的所有系数一个jξ(j = 0,±1,…,±5),并使它们等于0,我们就得到了代数方程集。在Maple的帮助下求解这些代数方程,我们有以下集合:
组1
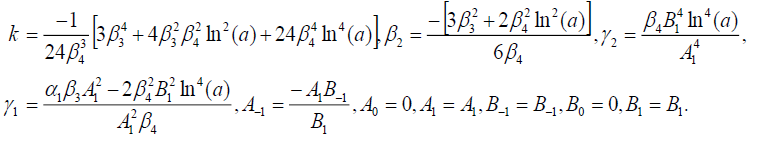 (100)
(100)
将式(100)代入式(69),得到式(42)的精确解:
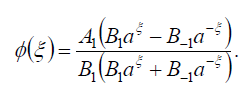 (101)
(101)
如果B-1=B1,则式(1)的暗孤子解为:
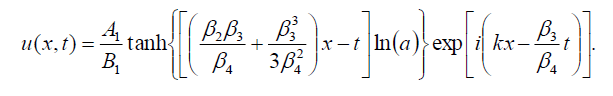 (102)
(102)
如果B-1=B1,则式(1)的奇异孤子解为:
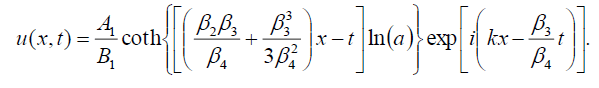 (103)
(103)
组2
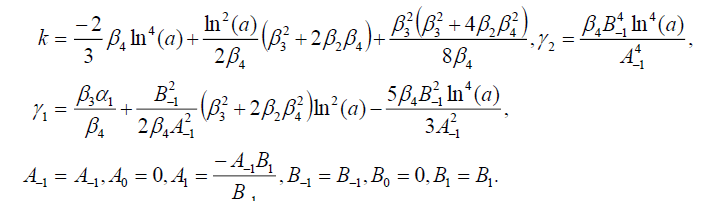 (104)
(104)
集合2的结果与集合1的结果有交换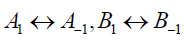 而且
而且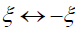 .
.
集3
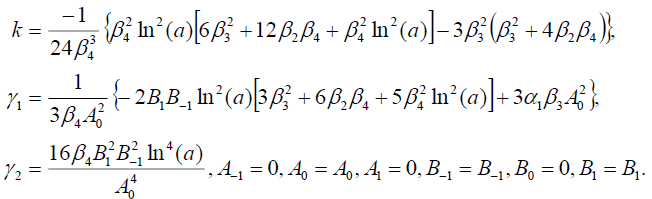 (105)
(105)
将式(105)代入式(69),得到式(42)的精确解:
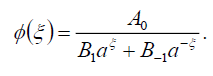 (106)
(106)
如果B-1=B1,则式(1)的亮孤子解为:
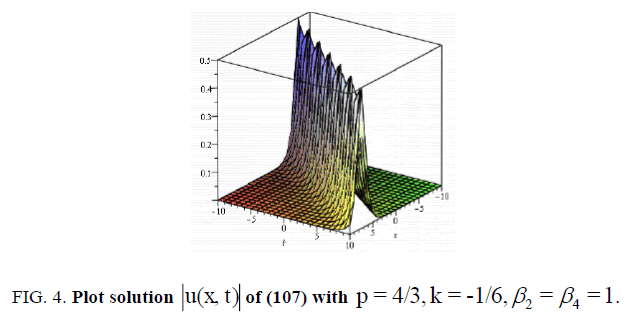
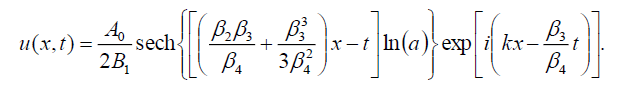 (107)
(107)
如果B-1=B1,则式(1)的奇异孤子解为:
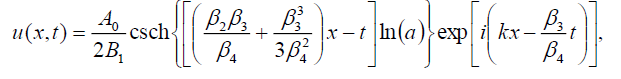 (108)
(108)
哪一个等价于前面的奇异孤子解(55),如果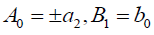 .
.
组4
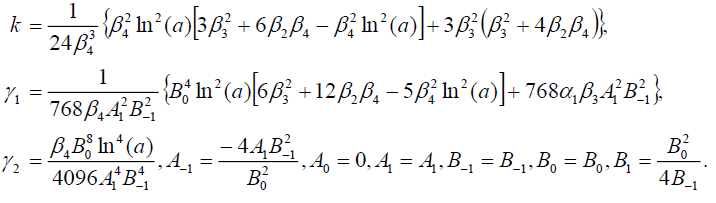 (109)
(109)
将式(109)代入式(69),得到式(42)的精确解:
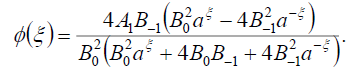 (110)
(110)
如果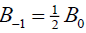 ,则式(1)的暗孤子解为:
,则式(1)的暗孤子解为:
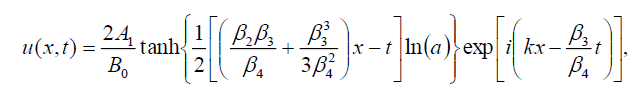 (111)
(111)
哪一个等价于前面的暗孤子解(59),如果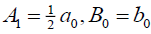 .
.
如果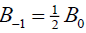 ,则式(1)的奇异孤子解为:
,则式(1)的奇异孤子解为:
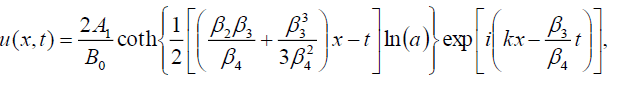 (112)
(112)
哪一个等价于前面的奇异孤子解(60),如果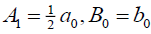 .
.
集合5
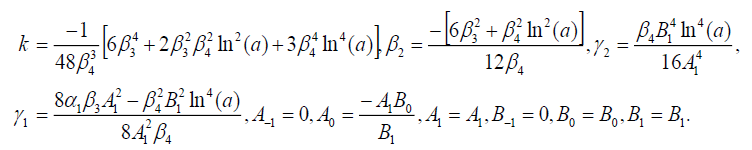 (113)
(113)
将式(113)代入式(69),得到式(42)的精确解:
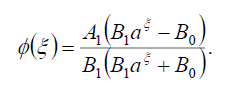 (114)
(114)
如果,B0=B1,则式(1)的暗孤子解为:
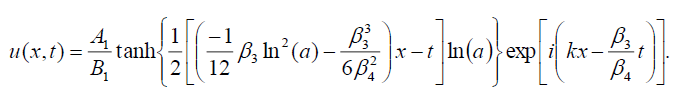 (115)
(115)
如果B0= -B1,则式(1)的奇异孤子解为:
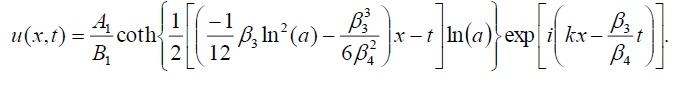 (116)
(116)
一些解的图形表示
在本节中,我们将说明上述结果的应用。结果的精确解描述了不同的非线性波。对于已建立的具有对称双曲斐波那契函数的明孤子解、暗孤子解和奇异孤子解是一类特殊的孤子波。光孤子解、暗孤子解和奇异孤子解有一个显著的特性,即在相互作用时保持其同一性。
现在让我们来研究一下图。1,2,3.而且4因为它说明了我们在本文中获得的一些结果。为此,我们选取了所得到参数的一些特殊值,例如具有四阶色散和三次五次非线性a的非线性Schrödinger方程的奇异、暗、亮孤子解(27)、(55)、(73)和(107)2= b0= b1=一个0=一个1= B1= c =α1=β3.-1, a = e,-10 < x, t <10。
结论
在本文中,我们证明了对称双曲Fibonacci函数解可以用广义Kudryashov方法和一般的Exp得到α函数的方法。作为应用,我们得到了许多新的四阶色散、三次-五次非线性非线性Schrödinger方程的精确解、对称双曲Fibonacci函数解以及明孤子解、暗孤子解和奇异孤子解。通过比较我们在本文中使用这些不同方法得到的结果与在[34-36]使用不同的方法,我们得出结论,我们对式(1)的结果是新的,没有在其他地方发表过。此外,本文所使用的不同方法对于求解各种非线性问题的精确解、孤波解和孤子解都是非常有效的技术。最后,我们在本文中得到的结果借助Maple进行了检验,将其重新放入原来的Eq.(1)中。
参考文献
- 孤子多次碰撞KdV方程的精确解。物理学报,1971;27:1192-4。
- Biswas EV。Krishnan, Ostrovsky方程的精确解。印度物理学报,2011;85:1513-21。
- 何建华,吴晓辉。非线性波动方程的表达式函数法,混沌孤子形,2006;30:70 -08。
- 阿斯兰。对expo -function方法及其应用的一些评述:补充。公共理论,2013;60:521-5。
- Yusufoglu AE。Bekir马。利用正余弦法求解Kawahara方程的周期和孤波解,混沌孤子,2008;37:1193-7。
- 泽丹·哈,摩纳哥SJ。Davey-Stewartson方程的正余弦法。:数学。E-Notes。2010; 10:103-11。
- 范娥,张华。齐次平衡法的一个注记。物理学报,1995;246:403-06。
- Zayed EME, Arnous AH。采用均相平衡法研究DNA动力学。下巴PhysLett。2011; 29:080203-05。
- Malfliet W, Hereman W. tanh方法:2。保守系统的摄动技术。物理学报,1996;54:569-75。
- tanh方法:sin - gordon方程和sin - gordon方程的精确解。应用数学与计算机。2005;37(2):344 - 344。
- 范娥,杨灿议员将广义tanh方法推广到特殊类型的非线性方程。中华自然科学杂志,2002;
- Abdou马。扩展tanh法及其在求解非线性物理模型中的应用。:数学。第一版。2007;190:988 - 96。
- 王敏,李霞,张军。(G’/G)展开法和非线性行波解进化数学物理方程。物理学报,2008;32:417-23。
- Zayed EME, Gepreel KA。(G’/G数学物理中求非线性偏微分方程行波解的展开法。物理学报。2009;50:013502-13。
- 扎耶德电磁辐射。高维非线性问题的新行波解进化使用广义(G’/G) -扩展方法。《物理与数学理论》。2009;42:195202-14。
- 贾瓦德JM, PetkovicAMD。非线性问题的修正简单方程法进化方程。:数学。Comput.2010; 217:869 - 77。
- Zayed EME, al - nowewhy AG。本文提出了改进的简单方程法α-函数法和求解长短波共振方程的孤子散射法。中国自然科学。2016;71a:103-12。
- Zayed EME, al - nowewhy AG。提出了求解带源广义非线性薛定谔方程的修正简单方程法和孤子散射法。《数学研究》2016;9:235-44。
- 扎耶德EME, Amer YA, al - nowewhy AG。改进的简单方程法和多重运算α-函数法求解非线性分数阶Sharma-Tasso-Olver方程。数学应用学报,2016;32:793-812。
- 马文祥,黄涛,张勇。非线性微分方程的一种多元函数法及其应用。phy Script.2010; 82:065003。
- Zayed EME, al - nowewhy AG。倍数expα-函数法和线性叠加原理求解(2+1)维calogro - bogoyavlenski - schiff方程。ZNaturforsch。2015; 70: 775 - 9。
- El-Shiekh RM, al - nowewhy AG。求解变系数NLSE的积分方法。中华自然科学杂志,2013;
- Moatimid GM, El-Shiekh RM, al - nowewhy AG。无变系数约束的变系数二维伯格方程的新精确解。科学通报,2013;(4):1-7。
- Sarma K, Saha M, BiswasA。功率光学孤子法律非线性和哈密顿摄动:精确解。红外毫米波。2010;31:48 -56。
- 双幂Benjamin-Bona-Mahoney方程的1孤子解法律非线性。数学与工程学报。2010;15(4):344 - 344。
- 谢伟科,陈志强,Güner Ö,等。暗-亮孤子解进化方程。数学与工程学报,2013;
- 周强,朱强,沙培库,等。抛物线中非线性色散的光学孤子法律媒介。Proc romania Acad Ser A. 2015;16:152-9。
- Zayed EME, al - nowewhy AG。(2+1)维双曲非线性Schrödinger方程的精确解和光孤子解。Optik。2016;127:4970 - 83。
- Zayed EME, Moatimid GM, al - nowewhy AG。广义Kudryashov方法及其在求解非线性偏微分方程中的应用。科学通报。2015;5:19-39。
- Zayed EME, al - nowewhy AG。用广义Kudryashov方法求了Biswas-Milovic方程、ZK(m,n,k)方程和k (m,n)方程的精确解。开放的今天。2016; 14:129-39。
- Zayed EME, al - nowewhy AG。用广义Kudryashov方法求解数学物理中非线性偏微分方程的精确行波解。中国电子学报,2016;13(2):203-27。
- 阿里T,哈桑ER。非线性的一般Exp函数法进化方程。应用数学计算。2010;217 451-9。
- Zayed EME, al - nowewhy AG。具有高阶非线性项的广义KdV-mKdV方程的孤子和其它解。J部分差异方程。2016;29:218-45。
- 张杰,戴凯。具有四阶色散和三次-五次非线性的非线性Schrödinger方程中的明暗光孤子。下巴光学列托人,2005:3:295-8。
- Hassan MM, Abdel-Wahab NH, Abdel-Daym MS.具有三次-五次非线性的高阶非线性薛定谔方程的精确解,自沉浸和自频移效应。应用数学学报。2016;26(3):495-513。
- Zayed EME, al - nowewhy AG。具有四阶色散和三次五次非线性的非线性Schrödinger方程的精确解和光孤子解。Ricerche mat.2017:1-22。
- Stakhov A, Rozin B.关于一类新的双曲函数。混沌孤子分裂。2005;23:379-89。